What Are Circle Theorems In Math?

Mathematics is a world filled with fascinating shapes, and one of the most captivating shapes in geometry is the circle. Circle theorems are essential principles that help us understand and work with circles effectively. In this comprehensive guide, we will delve into the world of circle theorems, demystifying their concepts and applications.

Circle Theorems Unveiled

The Circle’s Anatomy

Before diving into the theorems themselves, it’s crucial to understand the basic components of a circle. A circle consists of a central point called the center and all the points that are equidistant from the center, forming the boundary known as the circumference. Understanding this fundamental structure is key to grasping circle theorems.

What’s in a Radius?

The radius of a circle is the distance from the center to any point on the circumference. It plays a pivotal role in circle theorems, as it influences many properties of the circle. As the saying goes, “All roads lead to Rome,” in the world of circles, all measurements lead back to the radius.

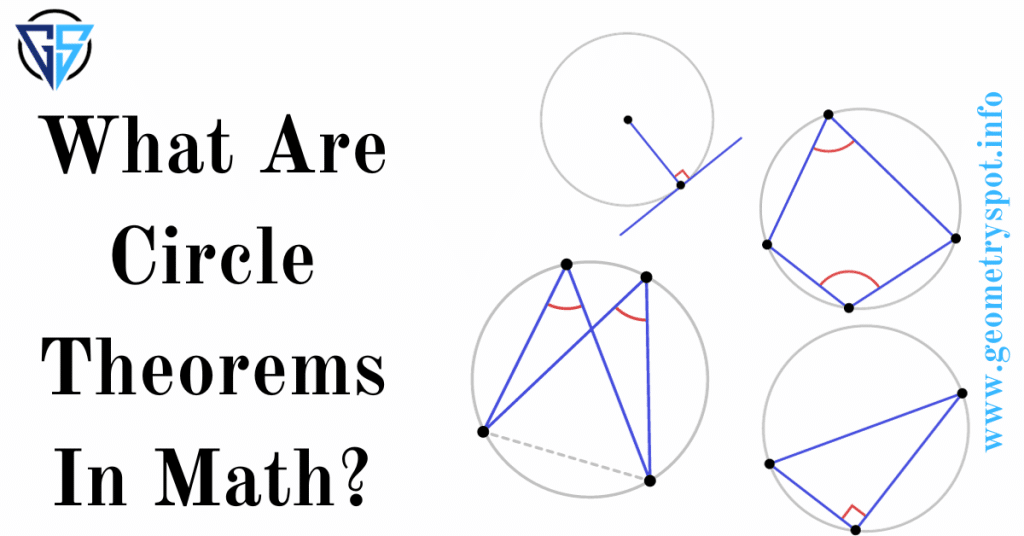
Inscribed Angles

Now, let’s explore one of the fundamental theorems involving circles – inscribed angles. An inscribed angle is an angle formed by two chords of the circle that intersect at the same endpoint on the circumference. It’s like catching two birds with one stone, as inscribed angles are directly proportional to the arcs they intercept.

Tangent Lines

Imagine a line that touches a circle at only one point, without crossing through it. This is called a tangent line. Tangent lines have a unique relationship with the radius at the point of tangency. They create a perfect right angle, making them essential players in circle theorems.

The Angle at the Center

Moving on to the center of attention, quite literally. The angle at the center theorem states that the angle formed at the center of a circle is twice the angle formed at the circumference, given the same arc. It’s like the circle’s way of doubling the fun!

Chord Length

Chords are segments that connect two points on the circle’s circumference. The chord length theorem reveals that if two chords are equidistant from the center, they are of equal length. This is a handy rule when working with various geometric problems involving circles.

Secants and Tangents

Secants are lines that intersect a circle at two distinct points, creating two segments. When a secant and a tangent line meet outside the circle, the angle formed is half the difference between the intercepted arcs. It’s a bit like finding the sweet spot in a game of darts!

FAQs

Q: Can you explain the concept of an inscribed angle in simple terms?

A: Of course! An inscribed angle is like an angle formed by two friends holding hands on the edge of a merry-go-round. It’s the angle between their outstretched arms, and it helps us understand the circle better.

Q: What’s the practical use of circle theorems?

A: Circle theorems are like tools in a mathematician’s toolbox. They help solve real-world problems involving circular objects, such as wheels, gears, and orbits.

Q: Why are tangents so important in circle theorems?

A: Tangents are like the secret agents of circles. They touch the circle at a single point and reveal critical information about its properties, making them essential in geometry.

Q: How can I remember all these theorems?

A: Mnemonics and practice are your best friends. Create catchy phrases or acronyms to remember the theorems, and solve lots of circle-related problems to reinforce your knowledge.

Q: Are circle theorems only for math enthusiasts?

A: Not at all! Circle theorems are like hidden gems in math. They may seem complex, but once you uncover their beauty, you’ll appreciate their elegance and usefulness in everyday life.

Q: Can you recommend any resources to learn more about circle theorems?

A: Absolutely! You can explore online tutorials, textbooks, and even seek guidance from your math teacher or tutor to delve deeper into this intriguing topic.

Conclusion

In the world of mathematics, circle theorems hold a special place. They are the keys that unlock the mysteries of circles, making them an essential part of geometry. Whether you’re a math enthusiast or someone looking to understand the world around you better, circle theorems are a valuable tool in your mathematical journey. So, embrace the world of circles, and let these theorems guide you on your mathematical adventures!